
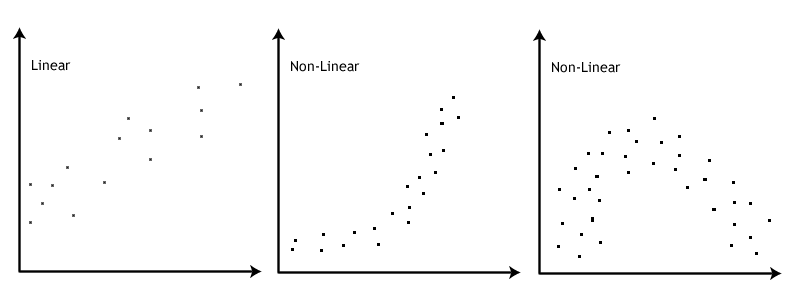
The scatter plot of Figure 9-1i illustrates a situation where as one variable increases in value, the other variable tends to decrease this can also be said about Figure 9-1d, but the relationship we see. In other words, when all the points on the scatter diagram tend to lie near a. In Figures 9-1a to 9-1h, we have seen scatter plots illustrating linear relationships of varying degrees of. The further away from the known x-values you are the less confidence you can have in the accuracy of the predicted y-values. Correlation is said to be non linear if the ratio of change is not constant. When you use a line or an equation to approximate a value outside the range of known values it is called linear extrapolation. For this you have to use a computer or a graphing calculator. To find the most accurate best-fit line you have to use the process of linear regression. If the data points come close to the best-fit line then the correlation is said to be strong. Approximately half of the data points should be below the line and half of the points above the line. If youre asked about 'positive' or 'negative' correlation, theyre. The word orrelation can be used in at least two different ways: to refer to how well an equation matches the scatterplot, or to refer to the way in which the dots line up. To help with the predictions you can draw a line, called a best-fit line that passes close to most of the data points. You may be asked about the 'correlation', if any, displayed within a particular scatterplot. If there is, as in our first example above, no apparent relationship between x and y the paired data are said to have no correlation and x and y are said to be independent.įrom a scatter plot you can make predictions as to what will happen next. If y tends to increase as x increases, x and y are said to have a positive correlationĪnd if y tends to decrease as x increases, x and y are said to have a negative correlation You can treat your data as ordered pairs and graph them in a scatter plot.Ī scatter plot is used to determine whether there is a relationship or not between paired data. nonlinear equation and how do we write the linear regression equation for a set of data using our calculator Homework: Handout.

Generate sample data: Fit regression model: Look at the results: Total running time.
You've summarized your result in a table. Toy example of 1D regression using linear, polynomial and RBF kernels. Let's say that you've the first of every month for one year been counting the amount of people on a subway platform each morning between 9 and 10 o'clock.


 0 kommentar(er)
0 kommentar(er)
